상업민족 페니키아인의 후예인 올리브유의 무역상인이기도 하였다. 선진국인 이집트나 바빌로니아 등에 여행하여 많은 과학적 지식을 익혔는데, 기원전 585년 5월 28일의 일식을 예언하기도 하고, 피라미드의 높이라든가 해안에서 해상의 배까지의 거리를 계산하였다.
또 변화가 많고 생명에게 있어서 없어서는 안되는 물을 형성하고 있는 시원물질이라 생각하고, 자연의 변전이나 다양성을 신화나 종교와 같은 초자연적, 신비적인 원리에서가 아니라, 자연 그 자체를 가지고 합리적·통일적으로 설명한 최초의 사람이다.
탈레스는 기원전 620년쯤에 그리스 이오니아 해안의 밀레토스라는 마을에서 태어났다. 그는 소금, 기름 등을 거래하는 상인으로 많은 재산을 모아 이집트에 유학하였다. 거기서 탈레스는 수학과 천문학을 배웠고, 피라미드의 높이를 짧은 막대 하나를 가지고 알아내 당시 사람들을 놀라게 하였다.
탈레스는 천문학에도 재능이 있어서, 그 당시에 이미 지구가 둥글다는 것을 알고 있었고, 1년이 365¼일이라는 것을 그리스에 소개하기도 하였다고 한다. 탈레스는 또 기원전 585년 5월28일에 일식이 일어날 것이며 메디아와 리디아의 전쟁이 이 일식 때문에 끝이 날 것이라고 예언하여 유명해지기도 하였다.
탈레스는 또 1) ‘맞꼭지각의 크기는 서로 같다’ 2) ‘이등변삼각형의 두 밑각의 크기는 서로 같다’ 3) ‘삼각형의 세 내각의 크기의 합은 180°이다’ 4) ‘반원에 내접하는 각은 직각이다’와 같은 많은 수학 명제를 증명하였다. 이러한 사실은 그 이전 사람들도 알고 있었고 중국 사람들도 알고 있었다.
그러나 탈레스는 이러한 성질이 어떤 특별한 한두 개의 삼각형이나 각에서 성립하는 것이 아니라 모든 삼각형이나 각에서 성립한다는 것을 ‘증명’하였다는 점에서 그리스 수학자의 시조로 불리고 있다. 천문에 관심이 많은 탈레스는 자주 하늘을 올려다보면서 연구에 열중하였다.
어느 날 저녁 밤하늘을 올려다보며 걷다가 바로 앞에 있는 웅덩이에 빠지고 말았다. 그것을 본 주변 사람들이 “바로 눈앞의 일도 알지 못하면서 어떻게 하늘에서 일어나는 일을 알 수 있는가”라고 빈정댔다고 한다. 그러나 바로 눈앞의 일이 아닌, 멀리, 높이 있는, 눈에 보이지 않는 것을 바라보며 그 일에 몰두하는 삶 때문에 탈레스가 지금도 유명하고 학문의 시조로 존경받게 되었다.
자세히
기원전 7세기 그리스 사람으로 만물은 물로 이루어졌다고 생각했다. 탈레스는 기원전 620년쯤에 그리스 이오니아 해안의 밀레토스라는 마을에서 태어났다. 그는 소금, 기름 등을 거래하는 상인으로 많은 재산을 모아 이집트에 유학하였다. 거기서 탈레스는 수학과 천문학을 배웠고, 피라미드의 높이를 짧은 막대 하나를 가지고 알아내 당시 사람들을 놀라게 하였다.
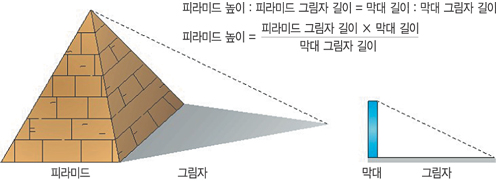
그러면, 탈레스는 피라미드의 높이를 어떻게 쟀을까? 피라미드의 그림자와 막대의 그림자를 재어 비례식으로 피라미드의 높이를 구했다고 한다. 그러나 어떤 사람은 탈레스가 피라미드의 높이를 다른 방법으로 구했다고 주장한다.
즉, 막대의 길이와 그림자의 길이가 같을 때 피라미드 그림자의 길이가 피라미드의 높이가 된다는 사실을 이용하여 피라미드의 높이를 구하였다는 것이다. 이것은 이등변삼각형의 성질을 이용한 것이다. 어떤 방법으로 피라미드의 높이를 재었든, 이집트의 아마시스 왕은 탈레스의 이 놀라운 재주에 무척 놀랐다고 한다.
탈레스는 천문학에도 재능이 있어서, 그 당시에 이미 지구가 둥글다는 것을 알고 있었고, 1년이 365¼일이라는 것을 그리스에 소개하기도 하였다고 한다. 탈레스는 또 기원전 585년 5월28일에 일식이 일어날 것이며 메디아와 리디아의 전쟁이 이 일식 때문에 끝이 날 것이라고 예언하여 유명해지기도 하였다.
탈레스는 또 1) ‘맞꼭지각의 크기는 서로 같다’ 2) ‘이등변삼각형의 두 밑각의 크기는 서로 같다’ 3) ‘삼각형의 세 내각의 크기의 합은 180°이다’ 4) ‘반원에 내접하는 각은 직각이다’와 같은 많은 수학 명제를 증명하였다.
이러한 사실은 그 이전 사람들도 알고 있었고 중국 사람들도 알고 있었다. 그러나 탈레스는 이러한 성질이 어떤 특별한 한두 개의 삼각형이나 각에서 성립하는 것이 아니라 모든 삼각형이나 각에서 성립한다는 것을 ‘증명’하였다는 점에서 그리스 수학자의 시조로 불리고 있다.
천문에 관심이 많은 탈레스는 자주 하늘을 올려다보면서 연구에 열중하였다. 어느 날 저녁 밤하늘을 올려다보며 걷다가 바로 앞에 있는 웅덩이에 빠지고 말았다. 그것을 본 주변 사람들이 “바로 눈앞의 일도 알지 못하면서 어떻게 하늘에서 일어나는 일을 알 수 있는가”라고 빈정댔다고 한다.